Proste filtry cyfrowe cz. 2. – filtr medianowy

W poprzednim wpisie zajmowaliśmy się jednym z najczęściej stosowanych prostych filtrów cyfrowych, czyli filtrem uśredniającym. Sprawdza się on w wielu wypadkach, jednak czasami słabo „radzi” sobie z chwilowymi szpilkami (zakłóceniami o dużej amplitudzie). W takim przypadku znacznie lepiej przefiltrujemy sygnał, jeśli zastosujemy filtr medianowy.
Czym jest filtr medianowy
Filtr medianowy to jeden z filtrów cyfrowych wykorzystywanych w przetwarzaniu sygnałów. Jego podstawowym zadaniem jest redukcja szumów z sygnału wejściowego poprzez wygładzenie sygnału i usuwanie wartości odstających od pozostałych.
Mediana to wartość, która dzieli zbiór danych na dwie równe części, tzn. połowę elementów ma wartość mniejszą, a drugą połowę większą od mediany. Aby obliczyć medianę, należy posortować zbiór danych od najmniejszej do największej wartości. Następnie, w zależności od parzystości liczby elementów w zbiorze, wyznaczana jest mediana:
- jeśli liczba elementów jest nieparzysta, to mediana to wartość środkowego elementu po posortowaniu zbioru,
- jeśli liczba elementów jest parzysta, to mediana to średnia arytmetyczna dwóch środkowych elementów po posortowaniu zbioru.
Filtr medianowy jest skuteczny w usuwaniu szumów impulsowych. Usuwa wartości odstające, ale nie modyfikuje kształtu sygnału, co jest ważne w przypadku sygnałów o dużej zmienności. Do zalet możemy również dodać, to, że jest prosty w implementacji.
Filtry medianowe nie są skuteczne w usuwaniu szumów o niskiej amplitudzie, co może być problemem w przypadku sygnałów o niskiej częstotliwości. Poza tym – podobnie jak filtr uśredniający, wprowadza opóźnienia do sygnału wyjściowego, co może być problematyczne w niektórych aplikacjach wymagających natychmiastowej reakcji na zmiany sygnału. Dodatkowo w przypadku dużych zbiorów danych, filtr medianowy może wymagać znacznej ilości pamięci co ma duże znaczenie dla aplikacji embedded.
Implementacja i przykład dla STM32
Poznaliśmy niezbędną dawkę teorii potrzebną do zrozumienia działania filtru. Przyjrzyjmy się przykładowi w języku C. Filtr medianowy zastosujemy w analogiczny sposób, jak filtr uśredniający – użyjemy go, aby przefiltrować dane otrzymane z pomiarów sygnałów analogowych, czyli wyjście z konwertera ADC. Jako źródło sygnału również wykorzystamy potencjometr.
Konfiguracja mikrokontrolera
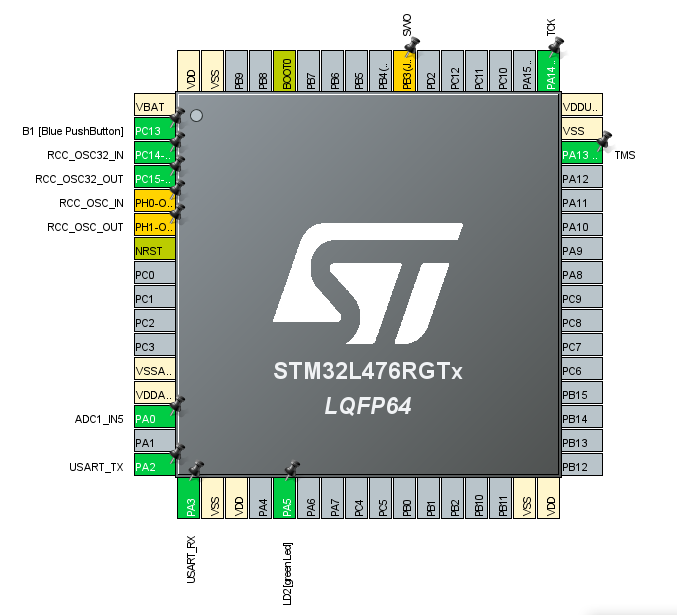
Do przykładu wykorzystamy mikrokontroler STM32L476RG dostępny w zestawie Nucleo-L476RG. Program napiszemy przy pomocy środowiska STM32CubeIDE.
Tworzymy nowy projekt wybierając „File->New->STM32 Project”. Przechodzimy przez wstępną konfigurację projektu i zabieramy się za konfigurację wyjść mikrokontrolera. Ja wygenerowałem projekt z domyślną konfiguracją dla płytki Nucleo, dlatego część pinów mam już skonfigurowane. Do obsługi potencjometru będziemy potrzebowali wejścia analogowego. W tej roli wykorzystamy wejście 5 przetwornika ADC1 (ADC1_IN5) podłączone do pinu PA0. Aby poprawnie skonfigurować pin, przechodzimy do zakładki po lewej stronie i wybieramy „Analog->ADC1”, a następnie przy wejściu IN5 wybieramy tryb „IN5 Single-ended” (tryb pomiaru na kanale ADC w odniesieniu do masy).
Teraz możemy przejść do konfiguracji ustawień przetwornika. Konwerter ADC w mikrokontrolerach STM32 to zaawansowany i dość rozbudowany system. Daje nam wiele możliwości, ale co za tym idzie, na początku trudniej jest się odnaleźć w „gąszczu” ustawień. Podstawowym wyborem jest wybór rodzaju konwersji. Mamy do dyspozycji dwa tryby: regularny (regular) i wstrzykiwany (injected). Podstawową różnicą jest to, że tryb wstrzykiwany ma wyższy priorytet i w przypadku wywołania jednoczesnej konwersji na kanale regularnym i wstrzykiwanym, to kanał wstrzykiwany będzie obsłużony w pierwszej kolejności. Poza wyniki konwersji kanałów wstrzykiwanych są przechowywane w indywidualnych rejestrach, a kanałów regularnych w jednym wspólnym rejestrze, który trzeba dostatecznie szybko odczytać, aby nie został nadpisany przez kolejny pomiar. Do naszego zastosowania w zupełności wystarczy nam konwersja w trybie regularnym.
Wśród podstawowych ustawień przetwornika ADC możemy wyróżnić:
- Ustawienia ogólne ADC (ADC Settings):
- Clock Prescaler – dzielnik zegara taktującego przetwornik. Wyższa wartość spowoduje, że pomiary będą wykonywane wolniej.
- Resolution – rozdzielczość pomiaru (6, 8, 10 lub 12 bitów).
- Data alignment – sposób wyrównania bitów danych w rejestrze wyjściowym (do prawej lub do lewej).
- Scan Conversion Mode – tryb skanowania dostępny w przypadku wykonywania pomiarów na kilku kanałach. Powoduje, że pomiar wykonywany jest na całej grupie kanałów jeden po drugi, czyli po wykonaniu pomiaru na jednym kanale, przetwornik automatycznie wykona pomiar na kolejnym (i tak aż przejdzie wszystkie kanały).
- Continuous Conversion Mode – tryb ciągły pomiarów, umożliwia automatyczne wystartowanie pomiarów na kanale (grupie kanałów) zaraz po ukończeniu poprzedniego.
- Discontinuous Conversion Mode – umożliwia wykonanie pojedynczo pomiarów w grupie. Powoduje, że po wykonaniu pomiaru na jednym kanale, przetwornik czeka na start konwersji i dopiero wykonuje pomiar na kolejnym.
- DMA Continuous Request – ustawia przesyłanie danych przez DMA w trybie ciągłym, czyli ADC generuje żądanie transferu DMA za każdym razem, gdy nowe dane są dostępne w rejestrze, nawet jeśli DMA wykonał ostatni transfer w grupie.
- End Of Conversion Selection – określa, jakie zdarzenie generuje ustawienie flagi końca konwersji (pojedyncza konwersja czy konwersja całej grupy).
- Ustawienia konwersji w trybie regularnym (ADC Regular Conversion Mode):
- Enable Regular Conversion – włącza tryb konwersji regularnej
- Nubmer of Conversion – określa liczbę konwersji do wykonania
- External Trigger Conversion Source – wybór zdarzenia, które będzie rozpoczynało konwersję
- External Trigger Conversion Edge – wybór zbocza, na którym będzie następowało wywołanie konwersji
Dla każdej konwersji możemy indywidualnie ustawić takie parametry, jak:
- Channel – kanał pomiaru, możemy tutaj zdecydować w jakiej kolejności będą się wykonywały pomiary
- Sampling Time – czas pomiaru zapisany w cyklach zegara, im dłuższy czas, tym dane są dokładniejsze
Powyżej przedstawiłem tylko najważniejsze parametry, z których będziemy korzystali najczęściej przy konfiguracji ADC.
W naszym przypadku będziemy wykonywali pomiar tylko na jednym kanale. Aby zautomatyzować odczyt danych o odległości, wykorzystamy zewnętrzne źródło wyzwalania pomiarów w postaci timera, który co 100 ms generował sygnał dla ADC.
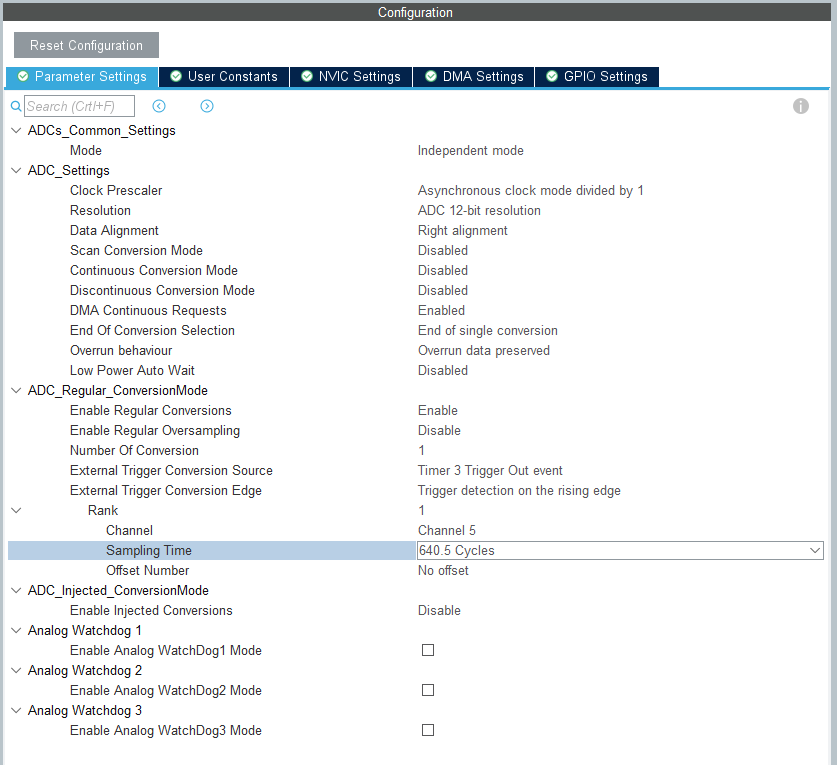
W celu poprawnego skonfigurowania przetwornika wybieramy zatem brak dodatkowego Prescalera, rozdzielczość 12-bitów oraz wyrównanie danych do prawej. Ponieważ mamy tylko jeden pomiar, nie będziemy potrzebowali trybu skanowania. Pomiar ADC będziemy chcieli mieć wywoływany co 10 ms przez timera, dlatego tryb ciągły też nie będzie nam potrzebny. Analogicznie nie potrzebujemy też trybu Discontinuous. Włączamy natomiast DMA Continuous Request Request i End Of Conversion Mode jako zakończenie pojedynczej konwersji.
W ustawieniach trybu regularnej konwersji, wybieramy zewnętrzne zdarzenie jako Timer 3 Trigger Out Event (czyli przepełnienie od timera 3 – lista dostępnych źródeł przerwań jest dostępna w liście rozwijanej obok parametru External Trigger Conversion Source oraz w dokumentacji „Reference Manual” na stronie 528 w tabeli 108.) oraz zbocze narastające. W ustawieniach pomieru wybieramy kanał 5 (wejście na pinie PA0) oraz najdłuższy czas konwersji, czyli 640,5 cykli, co zapewni nam większą dokładność. Pełna konfiguracja widoczna jest poniżej.
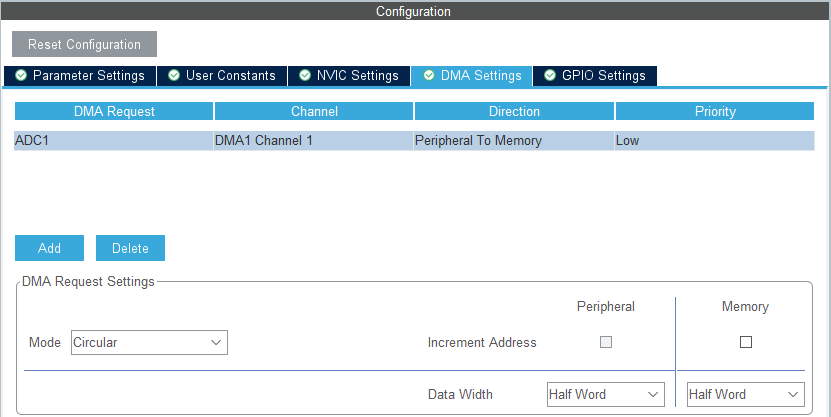
Żeby wykorzystać przesyłanie danych za pomocą DMA, w zakładce DMA Settings wybieramy ADC1 i DMA1 Channel 1. W ustawieniach może pozostać tryb Circular, bez inkrementacji adresów (mamy tylko jeden pomiar) oraz długość danych Half Word.
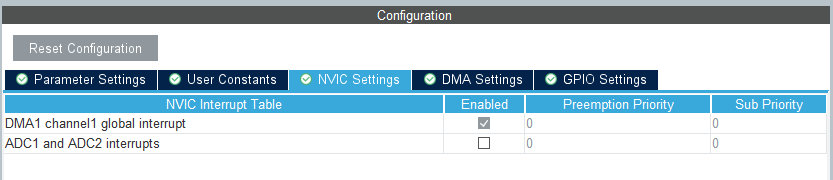
Na koniec włączamy jeszcze przerwania od DMA, dzięki czemu będziemy wiedzieli kiedy zakończył się pomiar, dane są gotowe w naszej zmiennej i można już wykonać filtrację.
Teraz powinniśmy skonfigurować jeszcze Timer 3 w taki sposób, aby wywoływał nam pomiar na ADC co 10 ms. Wybieramy zatem Timers->TIM3. W górnej części zaznaczamy Clock Source jako Internal Clock.
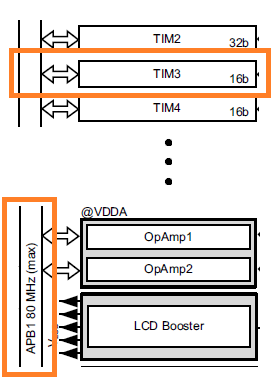
Aby skonfigurować licznik, musimy odpowiednio ustawić wartości: Prescaler i Counter Period. Potrzebujemy zatem informacji o częstotliwości taktowania Timera 3. Zgodnie z dokumentacją (Datasheet) mikrokontrolera na stronie 17, TIM3 podłączony jest do szyny taktującej APB1 i zgodnie z konfiguracją zegara, taktowany będzie z częstotliwością 80 MHz.
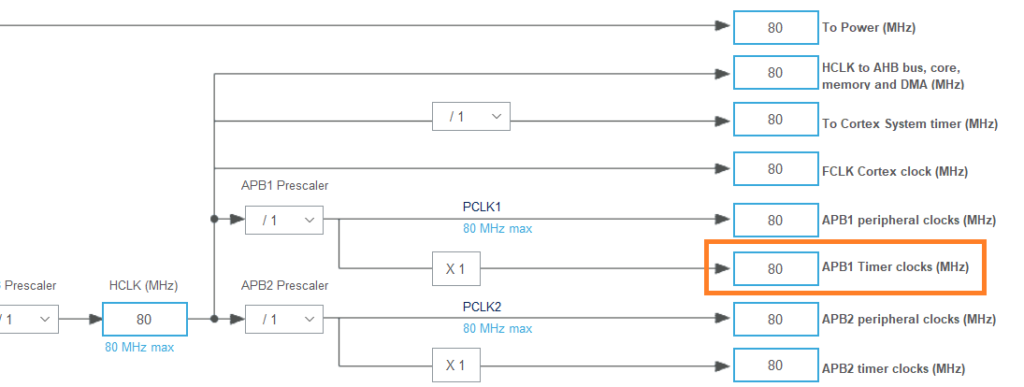
Zgodnie ze wzorem:
TIM_Freq = APB1_Freq / (Prescaler * Counter Period )
Aby uzyskać częstotliwość 100 Hz musimy podzielić zegar przez 800 000. Biorąc pod uwagę maksymalne wartości, jakie możemy wpisać do ustawień Prescaler i Counter Period, konfiguracja Timer 3 będzie wyglądała następująco:
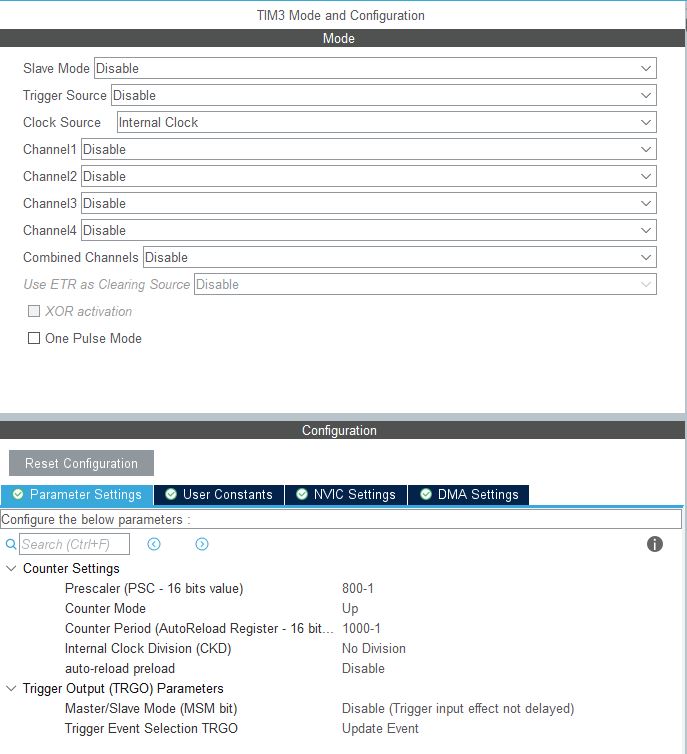
Aby Timer mógł generować zdarzenie dla ADC, zaznaczamy jeszcze opcję Trigger Event Selection TRGO jako Update Event. Widok wyjść mikrokontrolera w konfiguratorze będzie się przedstawiał jak na poniższym obrazku.
Przy tak skonfigurowanych peryferiach możemy wygenerować projekt („Project->Generate Code” lub „Alt+K„) i przejść do napisania kodu programu.
Filtr medianowy w języku C
Funkcja będzie składała się w trzech operacji. Najpierw musimy przesunąć dane w buforze tak, aby wypadła z niego najstarsza dana, a pojawiła się najnowsza. Potem powinniśmy posortować dane zapisane w buforze. Na koniec nasza funkcja musi zwrócić medianę z posortowanych pomiarów – będzie to przefiltrowana dana.
int32_t filter_median(int32_t new_data)
{
int32_t tmp_array[BUFFER_SIZE];
int32_t out = 0;
circular_buffer_push(&buffer, new_data);
memcpy(tmp_array, buffer.data, sizeof(tmp_array));
bubble_sort(tmp_array, BUFFER_SIZE);
out = get_median(tmp_array, BUFFER_SIZE);
return out;
}Podobnie jak w przypadku filtra uśredniającego, do przechowywania danych zastosujemy bufor kołowy. Dane będziemy dopisywali do bufora, jednocześnie zwiększając zmienną wskazującą na jego koniec. W momencie jak dojdziemy do końca tablicy, wrócimy na jej początek i będziemy nadpisywać najstarszą daną. Przy liczeniu średniej nie ma znaczenia w jakiej kolejności pobierzemy dane z bufora – wynik będzie taki sam. A zaoszczędzimy w ten sposób sporo czasu, ponieważ dodanie nowego pomiaru do bufora będzie polegało jedynie na zapisie jej w tablicy w odpowiednim miejscu.
Do obsługi bufora kołowego (Circular Buffer) wykorzystamy prostą strukturę przechowującą tablicę z danymi, zmienną z końcem bufora oraz rozmiar.
typedef struct
{
int32_t data[BUFFER_SIZE];
uint32_t head;
uint32_t size;
} circular_buffer_t;Na początku musimy zapewnić, że w tablicy nie ma żadnych przypadkowych danych. Zapisujemy również długość bufora do zmiennej oraz ustawiamy koniec bufora na zerowy element tablicy.
void circular_buffer_init(circular_buffer_t *buff)
{
buff->head = 0;
buff->size = BUFFER_SIZE;
for (uint32_t i=0; i < buff->size; i++)
{
buff->data[i] = 0;
}
}Dodanie danej do bufora będzie polegało na wpisaniu jej do tablicy w miejsce aktualnego końca bufora oraz zwiększenie licznika. Koniecznie musimy też sprawdzać, czy nie natrafiliśmy na koniec tablicy – pisanie po niezarezerwowanym obszarze pamięci może się skończyć HardFault-em, często trudnym do debugowania.
void circular_buffer_push(circular_buffer_t *buff, int32_t new_data)
{
buff->data[buff->head] = new_data;
buff->head++;
buff->head = buff->head % buff->size;
}Teraz musimy posortować dane. Temat sortowania danych jest bardzo powszechny wśród programistów. Znajdziemy wiele bardziej lub mniej wydajnych algorytmów. Ja zastosowałem proste sortowanie bąbelkowe.
static void bubble_sort(int32_t *array, int32_t size)
{
uint32_t i, j;
for (i = 0; i < (size - 1); i++)
{
for (j = 0; j < (size - i - 1); j++)
{
if (array[j] > array[j + 1])
{
swap(&array[j], &array[j + 1]);
}
}
}
}
static void swap(int32_t *xp, int32_t *yp)
{
int32_t temp = *xp;
*xp = *yp;
*yp = temp;
}Ostatnim etapem jest wyznaczenie mediany w posortowanej tablicy. Zgodnie z teorią, w zależności czy rozmiar tablicy jest liczbą parzystą czy nieparzystą, liczy średnią z dwóch środkowych wartości lub dla rozmiaru nieparzystego zwracamy środkową wartość.
int32_t get_median(int32_t *array, int32_t size)
{
int32_t median;
if ((size % 2) == 0)
{
median = (array[size/2-1] + array[size/2]) / 2;
}
else
{
median = array[size/2-1];
}
return median;
}Przed rozpoczęciem filtrowania musimy jeszcze stworzyć nasz filtr oraz go zainicjalizować w funkcji main(). Do tego dodamy funkcję inicjalizacyjną oraz bufor, który posłuży do przechowywania danych z pomiarów.
circular_buffer_t buffer;
void filter_median_init(void)
{
circular_buffer_init(&buffer);
}Do przechowywania pomiaru z ADC (transfer DMA) oraz przefiltrowanej wartości posłużą nam dwie zmienne globalne (umieściłem je w pliku main.c).
uint32_t adc_raw = 0;
volatile uint32_t adc_filtered = 0;W funkcji main() wywołujemy przed pętlą while(1) start pomiaru DMA oraz uruchamiamy Timer. Poza tym umieszczamy w niej inicjalizację filtru za pomocą zapisanej przed chwilą funkcji filter_moving_average_init().
HAL_ADC_Start_DMA(&hadc1, &adc_raw, 1);
HAL_TIM_Base_Start(&htim3);
filter_median_init();Następnie w obsłudze przerwania od transferu DMA wywołujemy filtrowanie danych.
void HAL_ADC_ConvCpltCallback(ADC_HandleTypeDef *AdcHandle)
{
adc_filtered = filter_median(adc_raw);
}Program gotowy. Czas przejść do sprawdzenia działania filtru. Pomiary obejrzymy sobie przy pomocy STM32CubeMonitor-a.
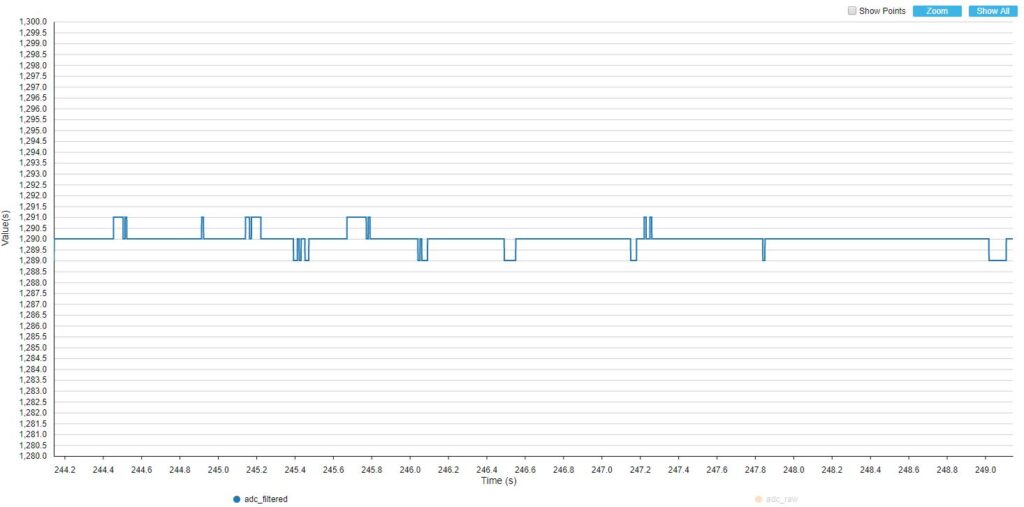
Zapisałem wykresy dla sygnału zarejestrowanego prosto z ADC oraz dla wyjścia filtru przy 10, 25 oraz 50 pomiarach wykorzystywanych do filtru (czyli inaczej długość bufora).
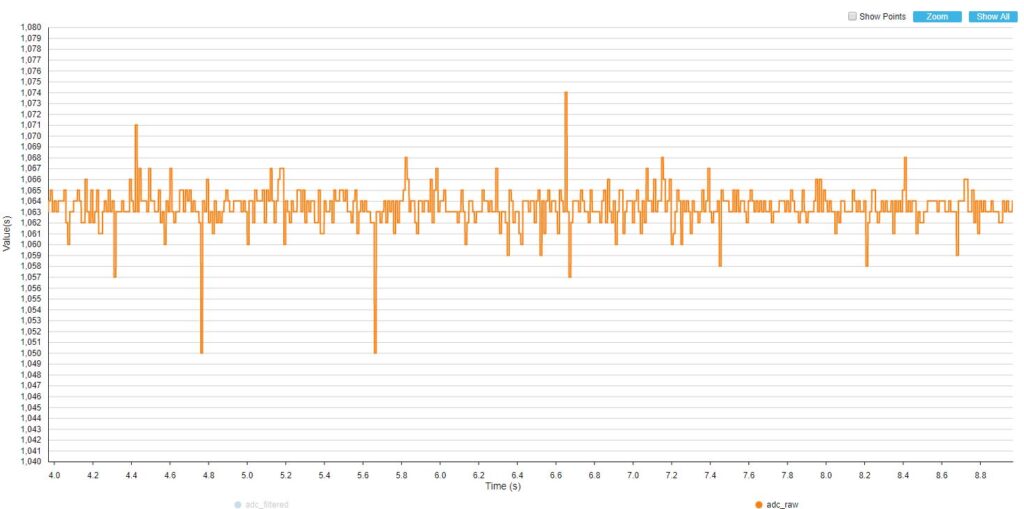
Jak można było się spodziewać, największe oscylacje są widoczne przy filtrze o najmniejszym buforze danych. Mimo wszystko nawet kilkuelementowy filtry potrafi skutecznie wygładzić dane. W przypadku filtru o długości 50 danych, zmiany na wyjściu są mało niewidoczne, chociaż trochę większe niż dla filtru uśredniającego.
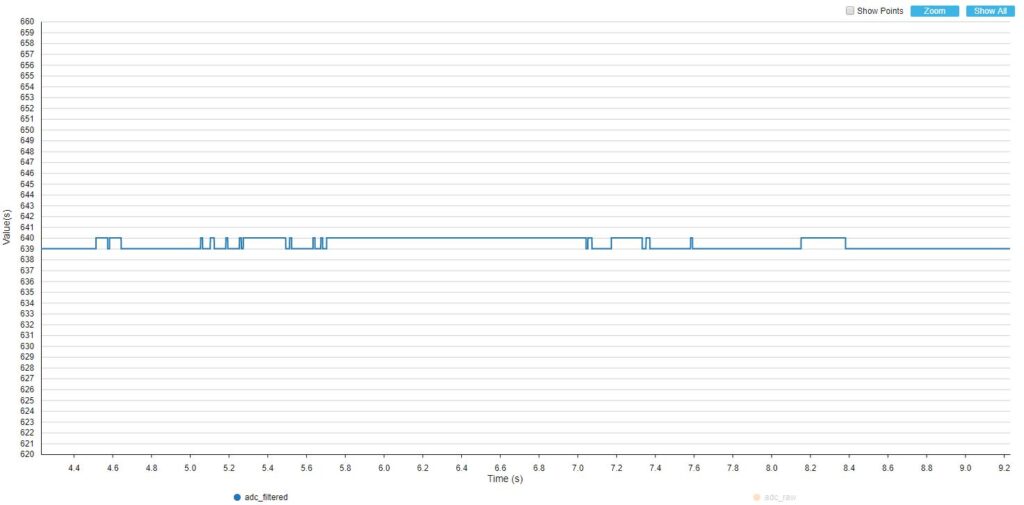
Podobnie jak w filtrze uśredniającym, długość bufora wpływa jednak nie tylko na jakość filtrowania. Zwiększanie ilości danych branych do liczenia średniej ma niestety także negatywny skutek. Spójrzmy jak będą wyglądały przebiegi w przypadku zmian położenia gałki potencjometru.
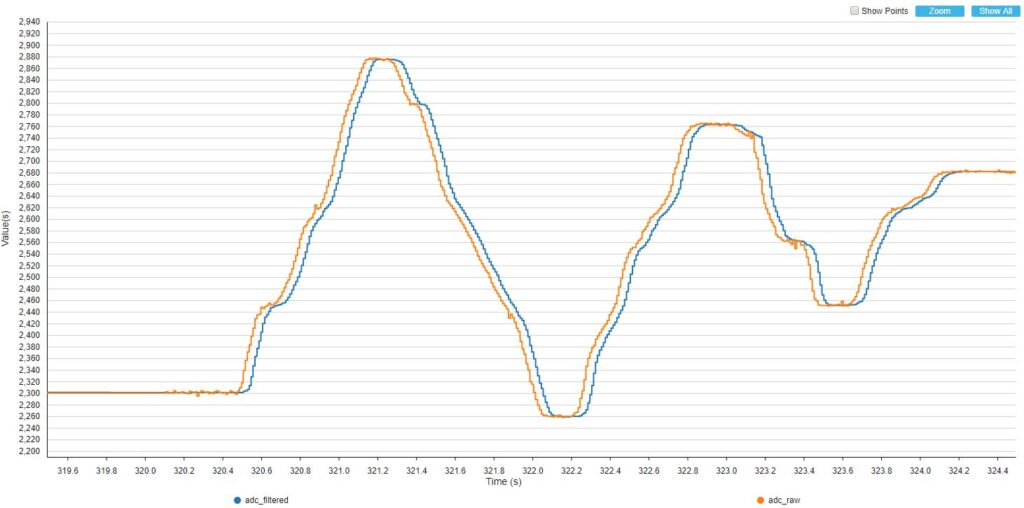
BUFFER_SIZE = 10 
BUFFER_SIZE = 25 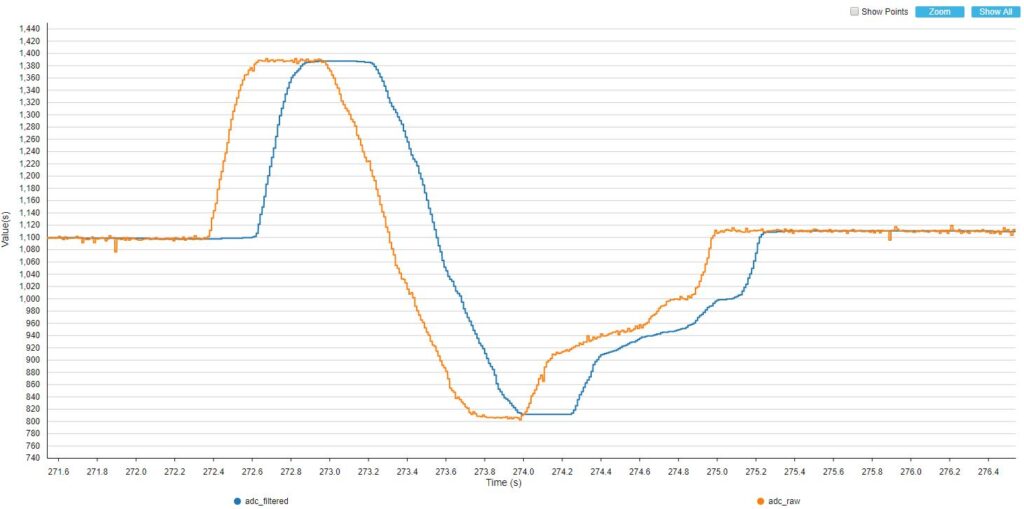
BUFFER_SIZE = 50
Im więcej danych w buforze, tym widoczne jest większe opóźnienie sygnału wyjściowego. Musimy tutaj dobierać wartości w zależności od tego, do czego stosujemy filtr.
Podsumowanie
W materiale przedstawiłem podstawowe założenia i zasadę działania filtru medianowego oraz jego implementację z języku C. Pokazane przykłady filtrowania sygnału potencjometru pokazują zarówno zalety, jak i wady działania prostego, ale przydatnego (szczególnie dla sygnałów, gdzie występują duże, chwilowe szpilki) filtru. Mam nadzieję, że dzięki artykułowi będzie Ci łatwiej wdrożyć prosty filtr medianowy do Twojego projektu.
Jeżeli wpis Ci się podobał, polub mój profil na Facebook-u oraz zasubskrybuj kanał na YouTube (linki znajdziesz na dole bloga). Projekt wykonany w ramach artykułu znajdzie na moim repozytorium GitHub.